'A BigBang produced...'

Table 2

This table gives indices for all the trees used in the paper.

Alpha Tubulin

Data Set	Chars	MP steps	Cons. steps	Trees	C.I.	R.I.	Isym
ATUBall	411	1346	1354	36	0.657	0.760	0.485
ATUB7	398	1206	1219	60	0.661	0.773	0.482
ATUB6	385	1092	1147	612	0.642	0.757	0.489
ATUB5	365	931	949	24	0.683	0.797	0.481
ATUB4	343	776	783	96	0.719	0.826	0.469
ATUB3	314	615	617	16	0.754	0.855	0.475
ATUB2	264	395	402	65	0.836	0.903	0.431
ATUB1	188	160	179	882	0.788	0.883	0.337
ATUB0	111	32	48	42	0.625	0.833	0.270

EF-1alpha

Data Set	Chars	MP steps	Cons. steps	Trees	C.I.	R.I.	Isym
EFall	388	1541			0.592	0.630
EF6	326	833	843	10	0.637	0.686	0.485
EF5	308	691	693	3	0.659	0.711	0.557
EF4	281	514	529	40	0.711	0.729	0.486
EF3	250	349	364	297	0.769	0.774	0.459
EF2	220	230	231	2	0.866	0.868	0.422
EF1	168	92	97	31	0.907	0.924	0.318
EF0	109	15	15	3	1.000	1.000	0.229

Small subunit RNA (transversions only, except first row)

Data Set	Chars	MP steps	Cons. steps	Trees	C.I.	R.I.	Isym
RNA-all	875	5043	5120	3432	0.29	0.628	0.302
RNAtv-all	875	2200	2208	1128	0.254	0.659	0.356
RNAtv6	801	1369	1436	> 10000	0.329	0.702	0.300
RNAtv5	771	1143	1245	8671	0.368	0.717	0.245
RNAtv4	743	972	1021	7964	0.403	0.733	0.199
RNAtv3	697	747	787	1062	0.463	0.772	0.206
RNAtv2	630	502	524	2076	0.556	0.822	0.158
RNAtv1	526	231	232	479	0.758	0.906	0.122
RNAtv0	376	25	25	2	1.000	1.000	0.063

Chars: Numbers of characters in the data set.

MP steps: Number of steps of the equiparsimonious trees.

Cons. steps: Number of steps of the consensus tree (might be different due to optimization).

Trees: Number of equiparsimonious trees.

C.I.: Consistency index.

R.I.: Retention index.

Isym: Index of symmetry.

Explanation of our index of symmetry

The common symmetry index from Heard et al. (Evolution 1992, 46:1818-1826) could not be used in our study because it has to be computed on perfectly dichotomic trees. We thus had to develop another index, in order to evaluate the symmetry of our many multifurcated trees.

We defined the order of emergence of a taxon as the number of nodes between that taxon and the root. For the purpose of our study, we defined the index of symmetry as the sum of the order of emergence of all taxa. This sum was then normalized (divided by n(n+1)/2 - 1, where n is the number of taxa) so that the maximal value is 1 (perfectly asymmetric tree).

We performed a comparison between the two indices, for 10,000 random dichotomic trees of 50 taxa. The result showed a strong positive correlation between the two indices, meaning that they provide a similar order relationship for dichotomic trees. As can be observed, our index does not reach 0 for dichotomic tree, hence the negligible plateau in the lower left corner.

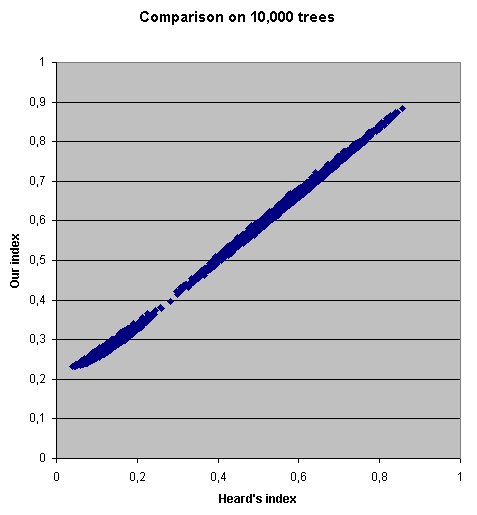
Though less intuitive than Heard's, our index allowed evaluate the symmetry of multifurcating tree. We nevertheless had to postulate that a radiation of 2ⁿ taxa (index 0) is more symmetric than the perfectly symmetric 2ⁿ taxa tree (index 2(n-1)/((2ⁿ+1)-1) ). Another disadvantage of our index is that one cannot compare the symmetry of trees with different numbers of taxa (as our index does not reach 0 for dichotomic trees).

Back to summary